%matplotlib inline
Training LeNet with Constrained Convolution Kernels#
In this part, we consider to train LeNet with constrained convolution kernals.
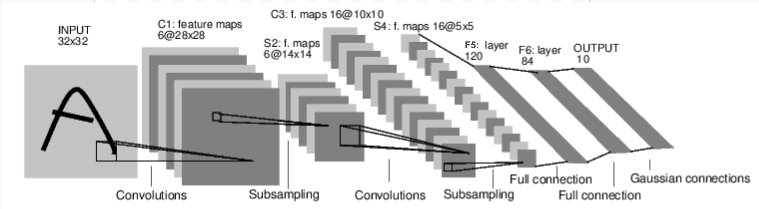
It is a simple feed-forward network. It takes the input, feeds it
through several layers one after the other, and then finally gives the
output. Such network can be constructed using the layers from torch.nn and cdopt.utils_torch.nn.
A typical training procedure for a neural network with constraints is as follows:
Define the neural network that has some learnable parameters (or weights), combined with layers from
cdopt.utils_torch.nnandtorch.nn.Define the loss function that evaluates how far is the output from being correct.
Design the traning and test processes.
Load dataset and set configs to the training process.
Train the neural network by optimizers from
torch.optim
This project may require the matplotlib and tqdm packages. You can install them through pip.
Importing modules#
We first import all the necessary modules for training LeNet.
import torch
import torch.nn as nn
import torch.nn.functional as F
import cdopt
from cdopt.nn.modules import Linear_cdopt, Conv2d_cdopt, get_quad_penalty
from cdopt.manifold_torch import stiefel_torch
Define the structure of the network#
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
# 1 input image channel, 6 output channels, 5x5 square convolution
# kernel, the `manifold_class` can be chosen as any manifold class provided in `cdopt.manifold_torch`
self.conv1 = Conv2d_cdopt(1, 6, 5, manifold_class=stiefel_torch, penalty_param=0.05)
self.conv2 = Conv2d_cdopt(6, 16, 5, manifold_class=stiefel_torch, penalty_param=0.05)
# an affine operation: y = Wx + b
self.fc1 = nn.Linear(256, 120) # 5*5 from image dimension
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
# Max pooling over a (2, 2) window
x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
# If the size is a square, you can specify with a single number
x = F.max_pool2d(F.relu(self.conv2(x)), 2)
x = torch.flatten(x, 1) # flatten all dimensions except the batch dimension
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
x = F.log_softmax(x, dim=1)
return x
net = Net()
print(net)
Net(
(conv1): Conv2d_cdopt(1, 6, kernel_size=(5, 5), stride=(1, 1))
(conv2): Conv2d_cdopt(6, 16, kernel_size=(5, 5), stride=(1, 1))
(fc1): Linear(in_features=256, out_features=120, bias=True)
(fc2): Linear(in_features=120, out_features=84, bias=True)
(fc3): Linear(in_features=84, out_features=10, bias=True)
)
Otherwise, users can uses the set_constraint_dissolving function from cdopt.nn.utils.set_constraints to set the manifold constraints to the convolution layers.
from cdopt.nn.utils.set_constraints import set_constraint_dissolving
class new_Net(nn.Module):
def __init__(self):
super(new_Net, self).__init__()
# 1 input image channel, 6 output channels, 5x5 square convolution
# kernel, the `manifold_class` can be chosen as any manifold class provided in `cdopt.manifold_torch`
self.conv1 = nn.Conv2d(1, 6, 5)
self.conv2 = nn.Conv2d(6, 16, 5)
# an affine operation: y = Wx + b
self.fc1 = nn.Linear(256, 120) # 5*5 from image dimension
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
set_constraint_dissolving(self.conv1, 'weight', manifold_class= stiefel_torch, penalty_param= 0.05)
set_constraint_dissolving(self.conv2, 'weight', manifold_class= stiefel_torch, penalty_param= 0.05)
def forward(self, x):
# Max pooling over a (2, 2) window
x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
# If the size is a square, you can specify with a single number
x = F.max_pool2d(F.relu(self.conv2(x)), 2)
x = torch.flatten(x, 1) # flatten all dimensions except the batch dimension
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
x = F.log_softmax(x, dim=1)
return x
net = new_Net()
print(net)
new_Net(
(conv1): ParametrizedConv2d(
1, 6, kernel_size=(5, 5), stride=(1, 1)
(parametrizations): ModuleDict(
(weight): ParametrizationList(
(0): manifold_module()
)
)
)
(conv2): ParametrizedConv2d(
6, 16, kernel_size=(5, 5), stride=(1, 1)
(parametrizations): ModuleDict(
(weight): ParametrizationList(
(0): manifold_module()
)
)
)
(fc1): Linear(in_features=256, out_features=120, bias=True)
(fc2): Linear(in_features=120, out_features=84, bias=True)
(fc3): Linear(in_features=84, out_features=10, bias=True)
)
Training the Network#
Then we define the training and testing process of the network.
def train(args, model, device, train_loader, optimizer, epoch):
model.train()
for batch_idx, (data, target) in enumerate(train_loader):
data, target = data.to(device), target.to(device)
optimizer.zero_grad()
output = model(data)
loss = F.nll_loss(output, target) + get_quad_penalty(model)
loss.backward()
optimizer.step()
if batch_idx % args.log_interval == 0:
print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
epoch, batch_idx * len(data), len(train_loader.dataset),
100. * batch_idx / len(train_loader), loss.item()))
def test(model, device, test_loader):
model.eval()
test_loss = 0
correct = 0
with torch.no_grad():
for data, target in test_loader:
data, target = data.to(device), target.to(device)
output = model(data)
test_loss += F.nll_loss(output, target, reduction='sum').item() # sum up batch loss
pred = output.argmax(dim=1, keepdim=True) # get the index of the max log-probability
correct += pred.eq(target.view_as(pred)).sum().item()
test_loss /= len(test_loader.dataset)
print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
Set parameters and options#
class ARGS():
pass
args = ARGS()
args.batch_size = 64
args.test_batch_size = 1000
args.epochs = 5
args.lr = 0.5 # learning rate
args.gamma = 0.7 # weight-decay parameter
args.no_cuda = False # whether use cuda
args.seed = 1 # random seed for traning
args.log_interval = 200 # the interval to print trainning information
args.save_model = False # whether to save the model
import torch.optim as optim
from torch.optim.lr_scheduler import StepLR
from torchvision import datasets, transforms
use_cuda = not args.no_cuda and torch.cuda.is_available()
torch.manual_seed(args.seed)
device = torch.device("cuda")
train_kwargs = {'batch_size': args.batch_size}
test_kwargs = {'batch_size': args.test_batch_size}
if use_cuda:
cuda_kwargs = {'num_workers': 1,
'pin_memory': True,
'shuffle': True}
train_kwargs.update(cuda_kwargs)
test_kwargs.update(cuda_kwargs)
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])
dataset1 = datasets.MNIST('../data', train=True, download=True,
transform=transform)
dataset2 = datasets.MNIST('../data', train=False,
transform=transform)
train_loader = torch.utils.data.DataLoader(dataset1,**train_kwargs)
test_loader = torch.utils.data.DataLoader(dataset2, **test_kwargs)
model = Net().to(device)
optimizer = optim.Adadelta(model.parameters(), lr=args.lr)
scheduler = StepLR(optimizer, step_size=1, gamma=args.gamma)
for epoch in range(1, args.epochs + 1):
train(args, model, device, train_loader, optimizer, epoch)
test(model, device, test_loader)
scheduler.step()
if args.save_model:
torch.save(model.state_dict(), "mnist_cnn.pt")
Train Epoch: 1 [0/60000 (0%)] Loss: 2.323270
Train Epoch: 1 [12800/60000 (21%)] Loss: 0.334674
Train Epoch: 1 [25600/60000 (43%)] Loss: 0.118695
Train Epoch: 1 [38400/60000 (64%)] Loss: 0.051988
Train Epoch: 1 [51200/60000 (85%)] Loss: 0.113355
Test set: Average loss: 0.0658, Accuracy: 9796/10000 (98%)
Train Epoch: 2 [0/60000 (0%)] Loss: 0.040481
Train Epoch: 2 [12800/60000 (21%)] Loss: 0.021898
Train Epoch: 2 [25600/60000 (43%)] Loss: 0.059031
Train Epoch: 2 [38400/60000 (64%)] Loss: 0.057162
Train Epoch: 2 [51200/60000 (85%)] Loss: 0.124436
Test set: Average loss: 0.0495, Accuracy: 9839/10000 (98%)
Train Epoch: 3 [0/60000 (0%)] Loss: 0.007051
Train Epoch: 3 [12800/60000 (21%)] Loss: 0.031250
Train Epoch: 3 [25600/60000 (43%)] Loss: 0.011009
Train Epoch: 3 [38400/60000 (64%)] Loss: 0.012897
Train Epoch: 3 [51200/60000 (85%)] Loss: 0.014972
Test set: Average loss: 0.0335, Accuracy: 9884/10000 (99%)
Train Epoch: 4 [0/60000 (0%)] Loss: 0.011187
Train Epoch: 4 [12800/60000 (21%)] Loss: 0.066403
Train Epoch: 4 [25600/60000 (43%)] Loss: 0.017215
Train Epoch: 4 [38400/60000 (64%)] Loss: 0.095960
Train Epoch: 4 [51200/60000 (85%)] Loss: 0.038313
Test set: Average loss: 0.0319, Accuracy: 9897/10000 (99%)
Train Epoch: 5 [0/60000 (0%)] Loss: 0.021864
Train Epoch: 5 [12800/60000 (21%)] Loss: 0.028929
Train Epoch: 5 [25600/60000 (43%)] Loss: 0.063708
Train Epoch: 5 [38400/60000 (64%)] Loss: 0.004671
Train Epoch: 5 [51200/60000 (85%)] Loss: 0.025337
Test set: Average loss: 0.0327, Accuracy: 9901/10000 (99%)
[model.conv1.quad_penalty(), model.conv2.quad_penalty()]
[tensor(6.4334e-06, device='cuda:0', grad_fn=<SumBackward0>),
tensor(0.0002, device='cuda:0', grad_fn=<SumBackward0>)]
Reference#
Hu X, Xiao N, Liu X, et al. A Constraint Dissolving Approach for Nonsmooth Optimization over the Stiefel Manifold[J]. arXiv preprint arXiv:2205.10500, 2022.