Training Multi-Layer RNN with Constrained Weights#
The multi-layer RNN are developed to create higher-level abstractions and capture more non-linearities between the data. With N_layer layers, multi-layer RNN has N_layer hidden states. Here is an example for two-layer RNN,
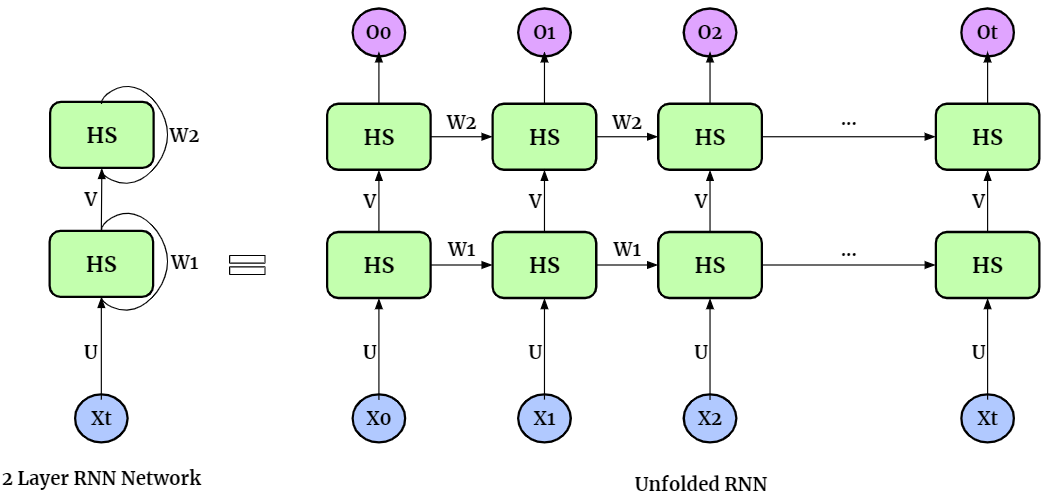
Similar to single-layer cases, when applied to the classification tasks on MNIST dataset, the structure of multi-layer RNN can be expressed as
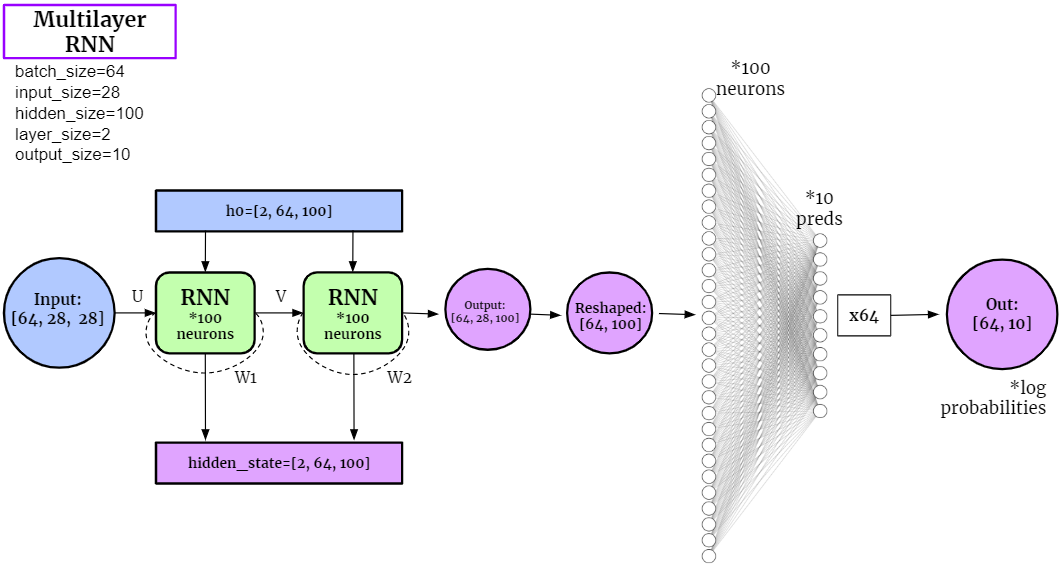
If we unfold the Multilayer RNN layer, it can be expressed as
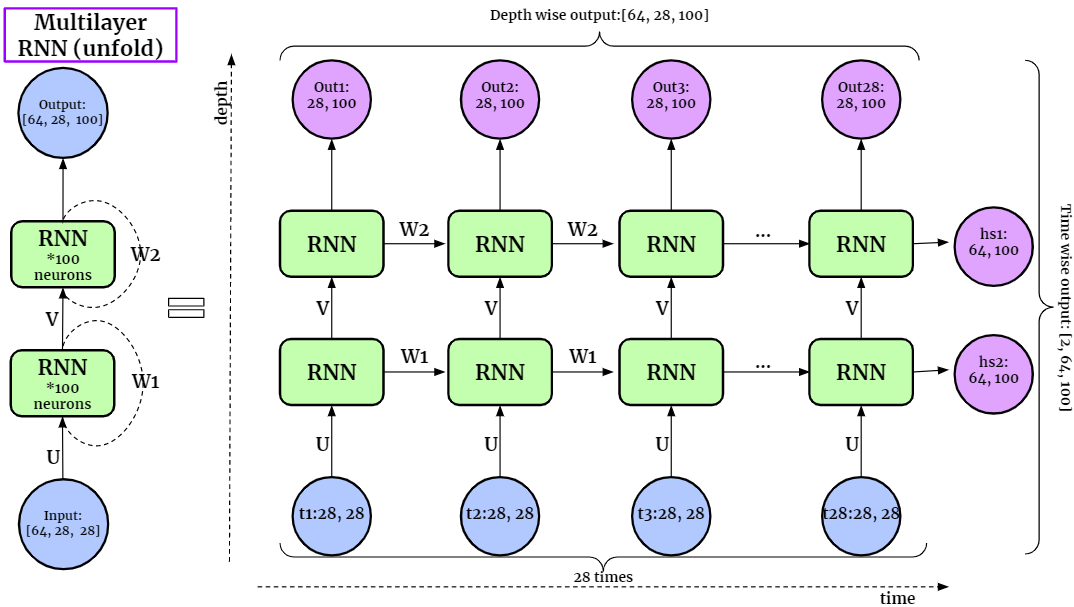
Import modules#
# Imports
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import os
import numpy as np
import torchvision
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
%matplotlib inline
import sklearn.metrics
import seaborn as sns
import random
from torch.nn.parameter import Parameter
# To display youtube videos
from IPython.display import YouTubeVideo
from cdopt.manifold_torch import euclidean_torch, stiefel_torch
from cdopt.nn import RNN_cdopt, get_quad_penalty
def set_seed(seed = 1234):
'''Sets the seed of the entire notebook so results are the same every time we run.
This is for REPRODUCIBILITY.'''
np.random.seed(seed)
random.seed(seed)
torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
# When running on the CuDNN backend, two further options must be set
torch.backends.cudnn.deterministic = True
# Set a fixed value for the hash seed
os.environ['PYTHONHASHSEED'] = str(seed)
set_seed()
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
print('Device available now:', device)
Device available now: cuda
Define the network#
Define a neurnal with constrained weights are quite simple via CDOpt, we only need the following two procedures:
Replace the layers in
torch.nnby the layers fromcdopt.utils_torch.nnand specify themanifold_classoptions.Add the
layer.quad_penalty()to the loss function.
class MultilayerRNN_MNIST(nn.Module):
def __init__(self, input_size, hidden_size, layer_size, output_size, relu=True):
super(MultilayerRNN_MNIST, self).__init__()
self.input_size, self.hidden_size, self.layer_size, self.output_size = input_size, hidden_size, layer_size, output_size
# Create RNN. Users can try other manifold classes from `cdopt.manifold_torch` in the setup of `cdopt.nn.RNN_cdopt`.
if relu:
self.rnn = RNN_cdopt(input_size, hidden_size, layer_size, batch_first=True, nonlinearity='relu', manifold_class = stiefel_torch, penalty_param = 0.2)
else:
self.rnn = RNN_cdopt(input_size, hidden_size, layer_size, batch_first=True, nonlinearity='tanh', manifold_class = stiefel_torch, penalty_param = 0.2)
# Create FNN
self.fnn = nn.Linear(hidden_size, output_size)
def forward(self, images, prints=False):
if prints: print('images shape:', images.shape)
# Instantiate hidden_state at timestamp 0
hidden_state = torch.zeros(self.layer_size, images.size(0), self.hidden_size).to(device)
hidden_state = hidden_state.requires_grad_()
if prints: print('Hidden State shape:', hidden_state.shape)
# Compute RNN
# .detach() is required to prevent vanishing gradient problem
output, last_hidden_state = self.rnn(images, hidden_state.detach())
if prints: print('RNN Output shape:', output.shape, '\n' +
'RNN last_hidden_state shape', last_hidden_state.shape)
# Compute FNN
# We get rid of the second size
output = self.fnn(output[:, -1, :])
if prints: print('FNN Output shape:', output.shape)
return output
Training RNN#
We’ll use
get_accuracy()andtrain_network()functions from the examples on Kaggle, but with some changes (suited to the RNN’s needs).
# Customized transform (transforms to tensor, here you can normalize, perform Data Augmentation etc.)
my_transform = transforms.Compose([transforms.ToTensor()])
# Download data
mnist_train = torchvision.datasets.MNIST('data', train = True, download=True, transform=my_transform)
mnist_test = torchvision.datasets.MNIST('data', train = False, download=True, transform=my_transform)
def get_accuracy(out, actual_labels, batchSize):
'''Saves the Accuracy of the batch.
Takes in the log probabilities, actual label and the batchSize (to average the score).'''
predictions = out.max(dim=1)[1]
correct = (predictions == actual_labels).sum().item()
accuracy = correct/batch_size
return accuracy
def train_network(model, train_data, test_data, batchSize=64, num_epochs=1, learning_rate=0.0005):
'''Trains the model and computes the average accuracy for train and test data.'''
print('Get data ready...')
# Create dataloader for training dataset - so we can train on multiple batches
# Shuffle after every epoch
train_loader = torch.utils.data.DataLoader(dataset=train_data, batch_size=batchSize, shuffle=True, drop_last=True)
test_loader = torch.utils.data.DataLoader(dataset=test_data, batch_size=batchSize, shuffle=True, drop_last=True)
# Create criterion and optimizer
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=learning_rate)
print('Training started...')
# Train the data multiple times
for epoch in range(num_epochs):
# Save Train and Test Loss
train_loss = 0
train_acc = 0
# Set model in training mode:
model.train()
for k, (images, labels) in enumerate(train_loader):
# Get rid of the channel
images = images.view(-1, 28, 28)
images = images.to(device)
labels = labels.to(device)
# print(labels.device)
# Create log probabilities
out = model(images)
# Clears the gradients from previous iteration
optimizer.zero_grad()
# Computes loss: how far is the prediction from the actual?
loss = criterion(out, labels) + get_quad_penalty(model)
# Computes gradients for neurons
loss.backward()
# Updates the weights
optimizer.step()
# Save Loss & Accuracy after each iteration
train_loss += loss.item()
train_acc += get_accuracy(out, labels, batchSize)
# Print Average Train Loss & Accuracy after each epoch
print('TRAIN | Epoch: {}/{} | Loss: {:.2f} | Accuracy: {:.2f}'.format(epoch+1, num_epochs, train_loss/k, train_acc/k))
print('Testing Started...')
# Save Test Accuracy
test_acc = 0
# Evaluation mode
model.eval()
for k, (images, labels) in enumerate(test_loader):
# Get rid of the channel
images = images.view(-1, 28, 28)
images = images.to(device)
labels = labels.to(device)
# Create logit predictions
out = model(images)
# Add Accuracy of this batch
test_acc += get_accuracy(out, labels, batchSize)
# Print Final Test Accuracy
print('TEST | Average Accuracy per {} Loaders: {:.5f}'.format(k, test_acc/k) )
# ==== STATICS ====
batch_size = 64
input_size = 28
hidden_size = 100
layer_size = 2
output_size = 10
# Instantiate the model
# We'll use TANH as our activation function
multilayer_rnn = MultilayerRNN_MNIST(input_size, hidden_size, layer_size, output_size, relu=False)
multilayer_rnn.to(device)
# ==== TRAIN ====
train_network(multilayer_rnn, mnist_train, mnist_test, num_epochs=10)
Get data ready...
Training started...
TRAIN | Epoch: 1/10 | Loss: 0.56 | Accuracy: 0.85
TRAIN | Epoch: 2/10 | Loss: 0.24 | Accuracy: 0.93
TRAIN | Epoch: 3/10 | Loss: 0.19 | Accuracy: 0.95
TRAIN | Epoch: 4/10 | Loss: 0.16 | Accuracy: 0.95
TRAIN | Epoch: 5/10 | Loss: 0.14 | Accuracy: 0.96
TRAIN | Epoch: 6/10 | Loss: 0.13 | Accuracy: 0.96
TRAIN | Epoch: 7/10 | Loss: 0.12 | Accuracy: 0.96
TRAIN | Epoch: 8/10 | Loss: 0.12 | Accuracy: 0.96
TRAIN | Epoch: 9/10 | Loss: 0.11 | Accuracy: 0.97
TRAIN | Epoch: 10/10 | Loss: 0.11 | Accuracy: 0.97
Testing Started...
TEST | Average Accuracy per 155 Loaders: 0.97016
multilayer_rnn.rnn.quad_penalty()
tensor(0.0024, device='cuda:0', grad_fn=<AddBackward0>)
Reference#
https://www.kaggle.com/code/andradaolteanu/pytorch-rnns-and-lstms-explained-acc-0-99
Jing L, Gulcehre C, Peurifoy J, et al. Gated orthogonal recurrent units: On learning to forget[J]. Neural computation, 2019, 31(4): 765-783.
Hu X, Xiao N, Liu X, Toh KC. A Constraint Dissolving Approach for Nonsmooth Optimization over the Stiefel Manifold[J]. arXiv preprint arXiv:2205.10500, 2022.